欧拉:难道他真的是数学界的“百科全书”吗?
欧拉:难道他真的是数学界的“百科全书”吗?
在数学的浩瀚星空中,瑞士数学家莱昂哈德·欧拉(Leonhard Euler,1707-1783)无疑是一颗璀璨的明星。他的成就不仅深刻影响了数学的发展,还为现代科学奠定了基础。有人说,欧拉是“百科全书般的数学家”,这究竟是怎样一种夸赞?他的贡献为何能让后人如此推崇?让我们一同探寻这位伟大数学家的传奇人生与卓越成就。
欧拉出生于瑞士巴塞尔的一个牧师家庭,早年便展现出过人的数学天赋。1717年,他进入巴塞尔大学,成为了当时最年轻的毕业生之一。在他短短的生命中,欧拉发表了超过800篇论文,涵盖了数学、物理学、天文学等多个领域,几乎没有哪个领域能逃过他的数学光芒。
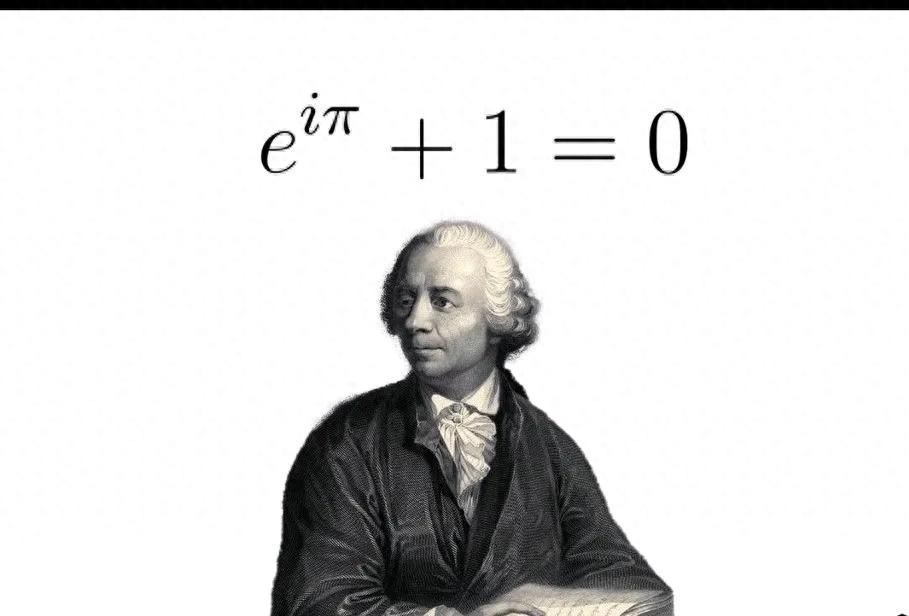
开启数学的新篇章
在18世纪的数学界,函数的概念尚未完全形成,许多数学家在表达数学关系时面临着重重困难。而欧拉的出现,犹如春风化雨,他不仅创立了“函数”这一重要概念,还为函数引入了符号。想象一下,在没有函数符号的时代,数学家们如何艰难地表达复杂的数学关系?正是欧拉的符号体系,使得数学表达变得简洁明了,极大地推动了数学的发展。
欧拉的著作《无穷小分析引论》更是奠定了微积分的基础,他通过严谨的推导和清晰的表述,让无穷小量的概念深入人心。这部作品不仅是微积分的经典之作,更是后世数学家学习和研究的重要参考。
科学的伟大飞跃
除了在纯数学领域的贡献,欧拉在物理学和工程学上的成就同样令人瞩目。他创立的分析力学,为经典力学提供了新的视角和方法。欧拉的方程,尤其是欧拉—拉格朗日方程,成为了现代物理学的基石。通过这些方程,科学家们能够更好地理解物体的运动规律,揭示了自然界的深层次法则。
在《微分学原理》中,欧拉详细阐述了微分方程的应用,特别是在物理问题中的应用。这本书的影响力延续至今,许多科学家在研究复杂系统时,仍然会借鉴欧拉的理论和方法。
数学的美与奇迹
提到欧拉,不能不提到他解决的柯尼斯堡七桥问题。这一问题源于普鲁士的柯尼斯堡(今加里宁格勒)城,城中有七座桥,居民希望找到一条可以走遍所有桥且不重复的路线。这个看似简单的问题,吸引了众多数学家的关注,但都无功而返。最终,欧拉以他独特的视角和严谨的逻辑,揭示了这一问题的本质,奠定了图论的基础。
欧拉在解决柯尼斯堡七桥问题时,提出了图的概念,开创了图论这一新领域。他的研究不仅为后来的数学家提供了重要的思路,也为计算机科学、网络理论等领域的发展提供了理论基础。
数学之美的典范
在欧拉的众多成就中,欧拉公式(Euler's formula)无疑是最具美感的。该公式将复数、指数和三角函数巧妙地结合在一起,展现了数学的和谐美。公式的表达为:\( e^{ix} = \cos(x) + i\sin(x) \)。这一公式不仅在理论数学中占据重要地位,也在工程学、物理学等领域中得到了广泛应用。
欧拉公式的美丽在于,它将看似无关的数学领域联系在一起,展现了数学的统一性和深刻性。”数学的美,正如这壮丽的自然景观,既深邃又神秘。
传承与创新
欧拉的著作不仅数量庞大,内容也极为丰富。他的《无穷小分析引论》和《微分学原理》是数学史上的里程碑,至今仍被广泛引用和学习。此外,欧拉在数论、几何、天文学等多个领域的研究,也为后来的数学家提供了重要的参考。
他的著作不仅具有理论价值,还强调了实际应用,这种理论与实践的结合,正是现代科学研究的核心理念。欧拉通过自己的努力,向世人展示了数学的力量与美丽。
永恒的数学传奇
在欧拉的身上,我们不仅看到了一个数学家的非凡才华,更看到了他对科学的热爱与执着。他的成就让我们深刻认识到,数学不仅仅是公式和定理的堆砌,更是一种思维方式,一种探索真理的工具。
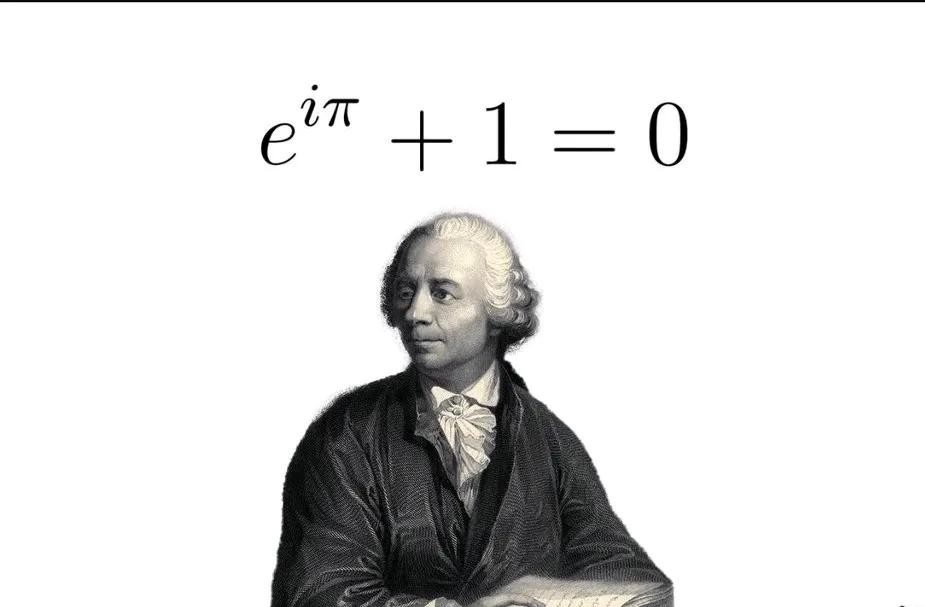
正如《离骚》中所言:“路漫漫其修远兮,吾将上下而求索。”欧拉用他的一生,诠释了这一精神。他的故事激励着无数后人追求知识、探索未知。在数学的海洋中,欧拉无疑是一座永恒的灯塔,指引着我们前行的方向。
那么,难道他真的是数学界的“百科全书”吗?答案显而易见,欧拉的成就与影响,早已超越了时代的界限,成为了数学史上不可磨灭的印记。#百家说史##历史##中外古今历史#
标签: